CC BY 4.0 (除特别声明或转载文章外)
课件下载 Lecture16
有时候我们需要将模型部署到其他算力较低的平台(手表,无人机……),这个时候就需要模型参数不能太大,我们就需要对我们的原模型进行网络压缩,在尽量保持模型效果的前提下,缩小模型的规模。
下面介绍五种算法层面的网络压缩,没有考虑硬件加速的部分。
Network Pruning

网络剪枝的大概流程是首先评估每个参数/神经元的重要性,将一部分重要性低的删除,删除后正确率肯定会降低,这时候我们做微调想办法提高正确率,尽量达到剪枝前的正确率,如此可以循环几次,直到小到符合我们需要的网络。注意一次不能删除太多参数/神经元,因为删除太多网络是无法通过微调恢复的。
Weight pruning

参数就是网络中各 Neuron 连接的部分,如果我们进行的是参数的剪枝,就是评估网络中每个连接的重要性,然后删除不重要的连接(上图左 -> 上图右)。但是这样就会造成网络不规则,我们很难在 Pytorch 中定义这种不规则的网络,而且我们很难使用 GPU 进行加速,因为 GPU 进行加速就是利用矩阵乘法,但是对于这种不规则的网络,很难转化为矩阵乘法。
由上述实验结果图可以看出来,Weight Pruning 是一个很厉害的方法,甚至可以剪枝掉 95% 的参数而 Accuracy 只降低 1-2%。按道理讲,网络 Pruning 了 95% 的参数,这么小的网络应该训练的很快才对,但是对于这种非规则网络根本就加速不起来,很多 Speedup 都小于 1,说明不是在加速反而是减速。
Neuron Pruning

神经元剪枝的优点就是保持规则的网络,方便 Pytorch 实操,可以 GPU 加速。但是这个剪枝的效率肯定比不过参数剪枝,因为一个神经元中有很多连接,对于神经元剪枝只能是这些连接重要性都比较低我们才可以删除掉这个神经元。但是对于参数剪枝,我们可以精准的删除神经元中不重要的连接,不用考虑这个神经元整体的情况。但是对于我们来说,还是神经元剪枝比较好,因为可以 GPU 加速(除非你自己写一个运算库,可以加速非规则网络)。
Why Pruning?
为什么我们不直接 Train 一个小的网络,而是先 Train 一个大的网络,然后再 Pruning 呢?原因在于如果你直接使用一个小网络很难 Train 起来,怎么解释呢?
有一个大乐透假说可以解释,注意是假说,不一定完全正确。他的观点就是每次训练网络的结果不一定会一样。我们抽到一组好的初始的参数,就会得到好的结果;抽到一组坏初始的参数,就会得到坏的结果。一个大网络就是很多小网络的组合,只要有一个小网络 Train 起来了,大网络就 Train 起来了,我们就可以开始 Pruning 不重要的部分。就像我们买彩票一样,买很多张比只买一张中奖率要高得多。
Knowledge Distillation

知识蒸馏算法是 Large Network 向 Small Network 传授知识。拿数字辨识任务举例,大小两个网络都是目标图片作为输入,Teacher Net 将输出的分布直接给 Student Net 作为标注,然后 Student Net 根据输入的图片和对应的分布进行训练。
比如教师的输出可能是看到这张图片 1 的分数是 0.7, 7 的分数是 0.2, 9 这个数字的分数是 0.1 等等。接下来给学生一模一样的图片,但是学生不是去看这个图片的正确答案来学习,它把老师的输出就当做正确答案,也就是老师输出 1 要 0.7, 7 要 0.2, 9 要 0.1。学生的输出也就要尽量去逼近老师的输出,尽量去逼近 1 是 0.7、 7 是 0.2、 9 是 0.1 这样的答案。
为什么知识蒸馏会有帮助呢?一个比较直觉的解释是教师网络会提供学生网络额外的信息,如果直接跟学生网络说这是 1,可能太难了。因为 1 可能跟其他的数字有点像,比如 1 跟 7 也有点像, 1 跟 9 也长得有点像,所以对学生网络,我们告诉它:看到这张图片我们要输出 1。 7 、 9 的分数都要是 0,可能很难,它可能学不起来,所以让它直接去跟老师学,老师会告诉它这是 1。我们没有办法让它是 1 分,也没有关系。其实 1 跟 7 是有点像的,老师都分不出 1 跟 7 的差别。老师说 1 是 0.7, 7 是 0.2,学生只要学到 1 是 0.7, 7 是 0.2 就够了。这样反而可以让小的网络学得比直接从头开始训练,直接根据正确的答案要学来得要好。
Hinton 论文里面甚至可以做到教师告诉学生哪些数字之间有什么样的关系这件事情,就可以让学生在完全没有看到某些数字的训练数据下,就可以把那一个数字学会。假设训练数据里面完全没有数字 7 ,但是教师在学的时候有看过数字 7 ,但是学生从来没有看过数字 7。但光是凭着教师告诉学生说 1 跟 7 有点像, 7 跟 9 有点像这样子的信息,都有机会让学生可以学到 7 长什么样子。就算它在训练的时候,从来没有看过 7 的训练数据。这是知识蒸馏的基本概念。
在使用知识蒸馏的时候有一个小技巧。这个小技巧是稍微改一下 Softmax 函数,会在 Softmax 函数中加一个温度(temperature)。Softmax 将网络的输出变成一个概率的分布,网络最终的输出都是介于 0 到 1 之间的。所谓温度,就是在做取指数之前,把每一个数值都除上 $T$。温度 $T$ 的作用就是把本来比较集中的分布变得比较平滑一点,这样学生才会更容易学到类别之间的联系。
Parameter Quantization
这个的核心思想就是通过减少参数的存储空间来实现压缩网络,比如原来一个参数需要 16 bits 但是处理后只需要 4 bits,网络的大小就直接缩小 4 倍。
- 最简单的方式是使用低精度的数据类型存储参数
- 参数聚类
举个例子,先对网络的参数做聚类,按照这个参数的数值来分群。数值接近的放在一群,要分的群数会先事先设定好,比如设定好要分四类。比较相近的数字就被当做是一类。每一类都只拿一个数值来表示它。比如黄色的类所有数字的平均值是 −0.4,就用 −0.4 来代表所有黄色的参数。储存参数时,就只要记两个东西:一个是表格,这个表格是记录说每一类代表的数值是多少。另外一个要记录的就是每一个参数属于哪一类。假设类的数量设少一点,比如说设四类,这样只要两个位就可以存一个参数了。
其实还可以把参数再更进一步做压缩,使用哈夫曼编码。哈夫曼编码的概念就是比较常出现的东西就用比较少的位来描述它,比较罕见的东西再用比较多的位来描述它。这样的好处平均起来,储存数据需要的位的数量就变少了。
Architecture Design
只学习其中一种,是关于 CNN 的一种变形,深度可分离卷积(Depthwise Separable Convolution)。我们先复习一下标准的 CNN。
在标准的 CNN 里面 input 的 channel 和 output 的 channel 数量可以不一样,这取决于你定义的 filter 的数量,一个 filter 会产生一个 output channel,但是每个 filter 里面的 channel 数量与 input 的 channel 数量保持一致。

在 Depthwise Convolution 中 input 有几个 channel 就有几个 filter,每个 filter 只负责一个 channel。但是单是这样还不够,因为这样会收集不到跨 channel 的特征。我们还需要加一个 Pointwise Convolution 专门负责跨 channel 的特征。
Pointwise Convolution 跟标准的 CNN 一样,输入和输出的 channel 可以不一样,但是限制就是每个 filter 的大小只能是 $1 \times 1$。也就是说只考虑跨 channel 的特征,而不看同一个 channel 中的特征(因为这是 Depthwise Convolution 的工作)。
计算得出 Depthwise Separable Convolution 相比与标准 CNN 参数量之间的关系是$\frac{1}{O} +\frac{1}{k \times k}$,因为 $O$ 通常是一个很大的值,通道数量可能设置为 256 或 512 ,所以先忽略 $O$, 所以这一整项的大小跟 $k \times k$是比较有关系的。假设核大小可能是 $3 \times 3$或者是 $2 \times 2$。假设核大小是 $2 \times 2$,把一般的卷积换成深度卷积加点卷积组合的话,网络大小就变成 $\frac{1}{4}$。假设核大小是 $3 \times 3$,从卷积变成深度卷积加点卷积的时候,网络大小就变成原来的 $\frac{1}{9}$。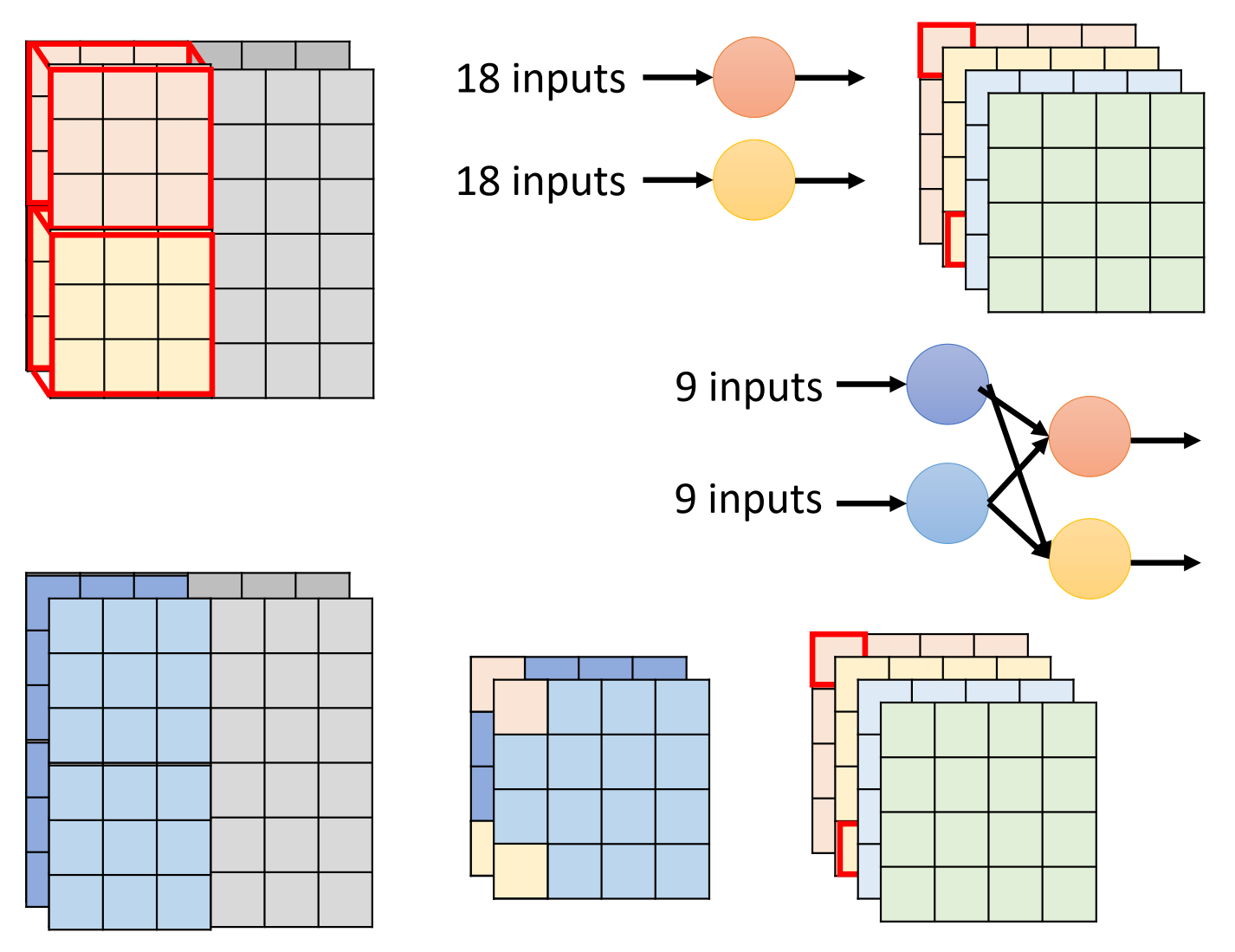
把原来 CNN 的一层变成了两层,先进行 Depthwise Convolution 再进行 Pointwise Convolution。
Dynamic Computation

我们期待模型可以自动调整它所需要的运算资源,因为有时候我们可能同样的模型会想要跑在不同的设备上面,而不同的设备上面的计算资源是不太一样的。举个例子,假设手机非常有电,可能就会有比较多的计算资源。所以期待训练好一个网络以后,放到新的设备上面,不需要再重训练这个网络。因为这个训练一个神奇的模型,这个神奇的模型本来就可以自由调整所需要的计算资源。计算资源少的时候只需要少的计算资源,就可以计算。计算资源大的时候,它就可以充分利用充足的计算资源来进行计算。
Dynamic Depth

怎么让网络自由地调整其对计算资源的需求呢?一个可能的方向是让网络自由地调整它的深度。比如图像分类,它就是输入一张图片,输出是图片分类的结果,可以在这个层和层中间再加上一个额外的层。这个额外的层的工作是根据每一个隐藏层的输出决定现在分类的结果。当计算资源比较充足的时候,可以让这张图片去跑过所有的层,得到最终的分类结果。当计算资源不充足的时候,可以让网络决定它要在哪一个层自行做输出。比如说计算资源比较不充足的时候,通过第一个层,就直接丢到这个额外的第 1 层,就得到最终的结果了。
一般在训练的时候,只需要在意最后一层网络的输出,希望它的输出跟标准答案越接近越好。但也可以让标准答案跟每一个额外层的输出越接近越好。把所有的输出跟标准答案的距离通通加起来,把所有的输出跟标准答案的交叉熵通通加起来得到 $L$,然后 minimize 这个 $L$就行。当然这是最简单的方法,不一定是最佳的方法。
Dynamic Width

图中的三个网络并不是三个不同的网络,它们是同一个网络可以选择不同的宽度。相同颜色是同一个权重。只是在最左边情况的时候,整个网络所有的神经元都会被用到。但是在中间情况的时候,可能会决定有 25% 的神经元不需要用。或者在最右边的情况, 50% 的神经元不要用它。在训练的时候,就把所有的情况一起考虑,然后所有的情况都得到一个输出,所有的输出都去跟标准答案计算距离,要让所有的距离都越小越好就结束了。
Computation based on Sample Difficulty

可以根据目标的难度来动态调整经过的层数。举例来说,如图所示,同样是猫,但有只猫是被做成一个墨西哥卷饼,所以这是一个特别困难的问题。也许这张图片只通过一个层的时候,网络会觉得它是一个卷饼;在通过第二个层的时候,还是一个卷饼。要通过很多个层的时候,网络才能够判断它是一只猫。这种比较难的问题就不应该在中间停下来。可以让网络自己决定这是一张简单的图片,所以通过第一层就停下来。这是一个比较困难的图片,要跑到最后一层才停下来,具体算法细节参考论文。
